안녕하세요. KataRN입니다.
항상 글을 써야지... 써야지... 하면서 미루게 되네요..
크흠...
오늘은 최단 거리를 구하는 알고리즘에 대해 써보려고 합니다.

저는 최단거리하면 6칸이면 aaa와bb로 나눠서 3! * 2! 했던 생각이 나네요...
하지만 이걸로는 풀수가 없었습니다... 흑흑...
자 우리는 이제 다음 단계로 넘어가봅시다.
우선 최단거리와 관련된 알고리즘이 2가지가 있습니다.
1. 다익스트라(Dijkstra)
2. 플로이드 워셜 알고리즘(Floyd Warshall Algorithm)
오늘은 2가지 모두 소개하려고합니다.
1. 다익스트라(Dijkstra)란?
- 음의 가중치가 없는 그래프의 한 정점(頂點, Vertex)에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘(최단 경로 문제, Shortest Path Problem)이다.
가능한 적은 비용으로 가장 빠르게 해답에 도달하는 경로를 찾아내는 대부분의 문제에 응용된다
이를 코드로 표현해보겠습니다.
아래는 기본정보 설정입니다.
//정점의 갯수
var n = 5
//시작 정점
var start = 1
//연결된 정보
var connections = [[1,2,1],[1,3,19],[1,4,10],[1,5,3],[2,3,30],[2,4,2],[2,5,7],[3,4,26],[3,5,4],[4,5,1]]
//경로를 저장할 배열
var allRoutes = (0...n).map{[$0]}
//거리를 저장할 배열(초기 값은 Int의 최댓값으로 설정)
var allDistances = Array(repeating: Int.max, count: n+1)
다음은 함수입니다.
//다익스트라로 시작 정점에서 가장 가까운 거리로 업데이트해줌.
func dijkstra() {
//자기 자신과의 거리는 0
allDistances[start] = 0
//시작 인덱스를 담은 큐를 만들어줌.
var queue:[Int] = [start]
//큐가 모두 없어질때까지 반복
while !queue.isEmpty {
//큐의 가장 첫번째 값을 저장하면서 삭제해줌.
let first = queue.removeFirst()
//연결 정보에서 큐의 첫번째 값이 있는 것들로 필터링 해줌.
let filterNodes = connections.filter{$0[0] == first || $0[1] == first}
//필터링한 것들을 순회
for node in filterNodes {
//첫번째 값이 아닌 것을 other로 설정
let connectionNode = node[0] == first ? node[1] : node[0]
//만약 Int 최댓값이라면 continue
if allDistances[first] == Int.max {continue}
//첫번째 값에 거리를 더한 것이 원래 있는 값보다 작다면
if allDistances[first]+node[2] < allDistances[connectionNode] {
//첫번째 값에 거리를 더한 것으로 업데이트
allDistances[connectionNode] = allDistances[first]+node[2]
//첫번째 큐에 있는 루트를 저장함.
var newRoute = allRoutes[first]
//현재 노드를 추가해줌.
newRoute.append(connectionNode)
//현재 노드를 새로운 경로로 바꿔줌.
allRoutes[connectionNode] = newRoute
//현재 노드를 큐에 넣어줌.
queue.append(connectionNode)
}
}
}
}다익스트라 알고리즘을 실행해주면 아래와 같이 allDistances엔 1에서 각 정점별 가장 짧은 거리가 담겨있고
allRoutes엔 가장 짧은 거리로 가는 경로가 순서대로 담기게 됩니다!
제가 테스트하면서 써본 코드입니다. 참고하시기 바랍니다.
func dijkstra(_ start: Int, _ N:Int, _ connections:[[Int]]) -> [Int] {
var allRoutes = (0...N).map{[$0]}
var allDistances = Array(repeating: Int.max, count: N+1)
allDistances[start] = 0
var queue:[Int] = [start]
while !queue.isEmpty {
let first = queue.removeFirst()
let filterNodes = connections.filter{$0[0] == first || $0[1] == first}
for node in filterNodes {
let connectionNode = node[0] == first ? node[1] : node[0]
if allDistances[first] == Int.max {
continue
}
if allDistances[first]+node[2] < allDistances[connectionNode] {
allDistances[connectionNode] = allDistances[first]+node[2]
//모든 최단루트
var newRoute = allRoutes[first]
newRoute.append(connectionNode)
allRoutes[connectionNode] = newRoute
//모든 최단거리
queue.append(connectionNode)
}
}
}
// return newRoute
return allDistances
}
2. 플로이드-워셜(Floyd-Warshall)이란?
플로이드-워셜 알고리즘(Floyd-Warshall Algorithm)은 그래프에서 가능한 모든 노드 쌍에 대해 최단 거리를 구하는 알고리즘이다.
다익스트라 알고리즘과는 달리 모든 노드 쌍에 대해 최단 거리를 구하고, 음의 가중치를 가지는 그래프에서도 쓸 수 있다는 것이 특징이다.
단순히 반복문을 3번 중첩시키기만 하면 되기 때문에 구현에 있어 크게 어려운 부분은 없다.
func 플로이드와샬() {
for i in 0..<N {
for j in 0..<N {
for k in 0..<N {
node[j][k] = min(node[j][i] + node[i][k], node[j][k])
}
}
}
}출처: https://nsios.tistory.com/130 [NamS의 iOS일기]
코드 길이 차이가 심한데?...
제가 테스트하면서 써본 코드입니다. 참고하시기 바랍니다.
func solution(_ N:Int, _ road:[[Int]], _ k:Int) -> Int {
var distance = [[Int]](repeating: [Int](repeating: 99999999, count: N), count: N)
for i in 0..<N {
distance[i][i] = 0
}
for i in road {
distance[i[0]-1][i[1]-1] = min(i[2], distance[i[0]-1][i[1]-1])
distance[i[1]-1][i[0]-1] = min(i[2], distance[i[1]-1][i[0]-1])
}
for k in 0..<N {
for i in 0..<N {
for j in 0..<N {
distance[i][j] = min(distance[i][j], distance[i][k] + distance[k][j])
}
}
}
return distance.first!.filter{$0<=k}.count
}위의 테스트 코드에 대해 추가설명 들어갑니다.
retrun값 전에 distance에 대해 설명드리겠습니다.
distance 는 [[1,2,3,],[1,2,3],[1,2,3]] 이렇게 N개의배열이 N개만큼 들어있는 배열입니다.
처음에는 각 값이 99999999로 들어가 있습니다.
그리고 플로이드가 적용되면
1번 배열에는 1->1, 1->2, 1->3으로 가는 최단거리값으로 바뀝니다.
2번 배열에는 2->1, 2->2, 2->3으로
3번 배열에는 3->1, 3->2, 3->3으로 바뀝니다.
이처럼 모든 마을간의 최단거리값을 넣는 코드입니다.
흠 비슷한듯 안비슷한 두 알고리즘....
결국 차이는 음의 가중치라는건데.. 뭔말이여...
음의 가중치란 B에서 C로 갈때 거리를 -로 한 경우입니다.(아래 그림 참조)
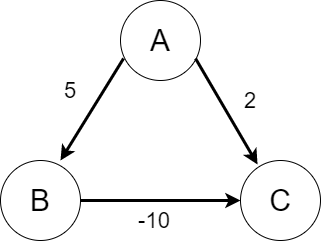
<아래 내용은 퍼왔습니다.>
플로이드: 각 정점간 최단경로를 구할 때
다익스트라: 시작점으로 부터 나머지 정점까지 최단거리를 구할 때
장단점
- 플로이드 알고리즘 소스가 훨씬 더 간결하다.
- 플로이드 알고리즘은 간선 수가 많으면 다익스트라 알고리즘보다 빠를 수가 있음.
- 시작점으로부터 각 정점까지 최단거리만 구해도 될 때, 보통 다익스트라 알고리즘이 압도적으로 빠름.
- 그래프에 음의 가중치 간선이 있으면(물론 음의 싸이클은 없어야 한다) 다익스트라 알고리즘은 못 쓰지만 플로이드 알고리즘은 사용할 수 있다.
사용전략
1. 정점간 최단경로를 모두 구해야 한다.
1-1. 간선이 매우 많다(V^2=E): 플로이드 알고리즘이 우수함.
1-2. 간선이 많지 않다:
플로이드 알고리즘은 V^3, 다익스트라 알고리즘은 VElogV 경우에 따라 다름
2. 시작점으로부터 나머지 정점까지 최단거리만 구해도 된다.
2-1. 간선이 매우 많다(V^2=E): 인접행렬을 이용하는 다익스트라 알고리즘을 사용한다.
2-2. 간선이 많지 않다: 인접리스트를 이용하는 다익스트라 알고리즘을 사용한다.
3. 최단경로를 구하는 것이 전체 시간에 큰 영향을 끼치지 않는다: 소스가 간결한 플로이드 알고리즘을 사용한다.
4. 그래프 간선에 음의 가중치가 존재한다: 다익스트라 알고리즘은 무조건 사용하지 못한다. 다른 최단경로 알고리즘과 비교한다.
출처: https://codedoc.tistory.com/95 [codedoc]
결국 같은 최단 경로를 구하는 코드인건 맞지만 어느것을 쓰는지는 상황에 따라 판단해야된다는 소리군요.
일반적으로는 다익스트라를 사용하며 가끔 플로이드가 빠름...
너무 대충... 마무리 지엇나..
다음의 나에게 보충설명을 넘기겠습니다..
오늘도 읽어주셔서 감사합니다.
'Old_SWIFT(221012) > 알고리즘이야기' 카테고리의 다른 글
| 백준에서 코딩테스트 해보기 (0) | 2022.02.20 |
|---|---|
| 우선순위 큐, 힙 구현하기 (0) | 2022.02.19 |
| DP(동적계획법) (0) | 2021.11.16 |
| DFS, BFS에 대해 알아봅시다. (0) | 2021.11.15 |
| 재귀함수, 꼬리재귀 (0) | 2021.11.15 |